Ojo! este post es un post de una convocatoria anterior, convocatoria 2019, que salió en el 2018.
Aquí están las soluciones del Simulacro 1 de Pronabec para el examen de preselección de Beca 18 - diciembre 2018!
Para ver la solución cada pregunta, hagan click en “Ver solución (hacer click aquí)” debajo de cada pregunta.
Muchas gracias al Profe Alex Z y a los voluntarios de OportuniDar!
Síguenos y comunícate con nosotros en la página: https://www.facebook.com/OportuniDarPeru/
(aquí la version PDF)
NÚMEROS Y OPERACIONES Y ESTADÍSTICA
1.- A un cine asisten 399 personas entre hombres, mujeres y niños.- El número de hombres es el quíntuplo del número de mujeres y este es el triple del número de niños. ¿Cuántos hombres hay?
(a) 21
(b) 63
(c) 325
(d) 315
Ver solución (hacer click aquí)

2.- Sí:
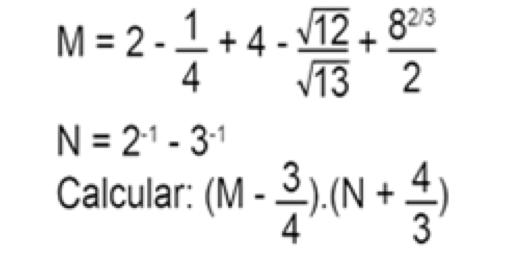
(a) 3/2
(b) 6,6
(c) 7,5
(d) 15/8
Ver solución (hacer click aquí)

3.- Sabiendo que E = A.B2, ¿cómo varía E si A disminuye 25% y B disminuye 20%?
(a) Disminuye 48%
(b) Disminuye 52%
(c) Disminuye 45%
(d) Disminuye 65%
Ver solución (hacer click aquí)

4.- Si al comprar tela me hubieran hecho un descuento del 15% en el precio, hubiera podido comprar 6 metros más. ¿Cuántos metros de tela compré?
(a) 34
(b) 40
(c) 42
(d) 45
Ver solución (hacer click aquí)

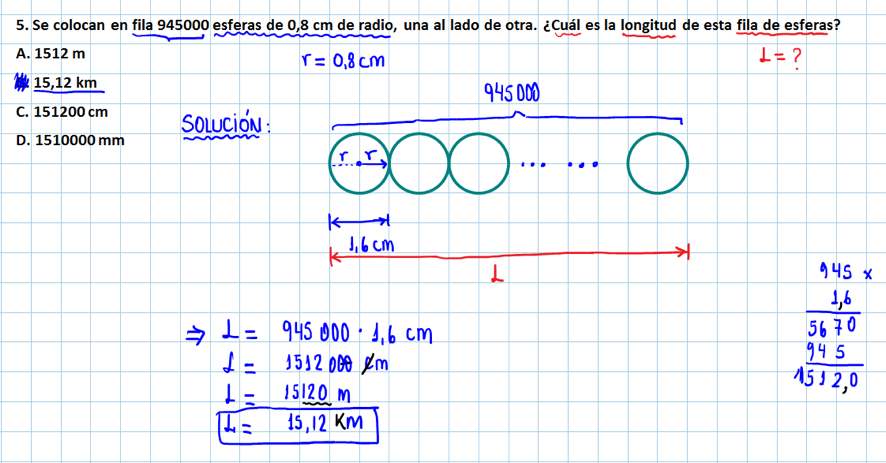
5.- Se colocan en fila 945000 esferas de 0,8 cm de radio, una al lado de otr(a) ¿Cuál es la longitud de esta fila de esferas?
(a) 1512 m
(b) 15,12 km
(c) 151200 cm
(d) 1510000 mm
Ver solución (hacer click aquí)
6.- Una compañía fabrica un producto tipo A cada 12 min, uno tipo B cada 18 min y uno tipo C cada 60 min. Si a las 3:30 am se empieza a fabricar un producto de cada tipo, ¿a qué hora volverán a fabricar un producto de cada tipo simultáneamente?
(a) 4:30 am
(b) 6:30 am
(c) 7:30 am
(d) 8:00 am
Ver solución (hacer click aquí)

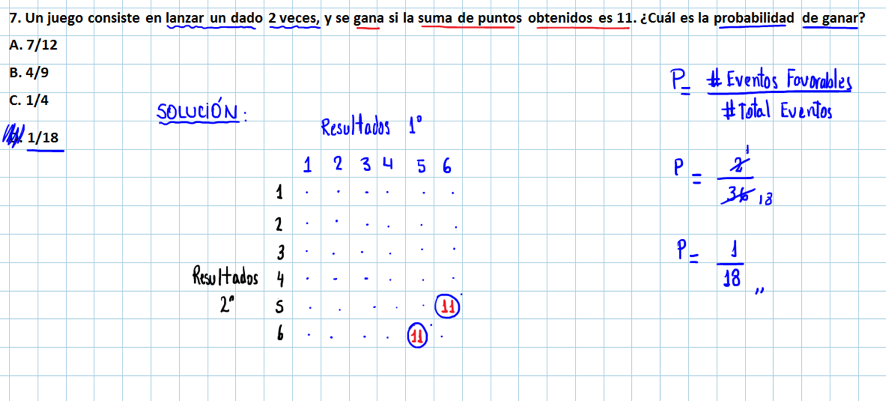
7.- Un juego consiste en lanzar un dado 2 veces, y se gana si la suma de puntos obtenidos es 11.- ¿Cuál es la probabilidad de ganar?
(a) 7/12
(b) 4/9
(c) 1/4
(d) 1/18
Ver solución (hacer click aquí)
8.- El promedio aritmético de cinco números es diez.- Si consideramos un sexto número, dicho promedio aumenta en dos unidades. Calcule el sexto número.
(a) 55
(b) 50
(c) 22
(d) 72
Ver solución (hacer click aquí)

9.- En la academia MAPRIS se desea comprar no más de 3 plumones para pizarra entre negros y rojos. Si se debe comprar al menos uno de cada color, ¿de cuántas maneras se puede efectuar la compra?
(a) 2
(b) 3
(c) 4
(d) 5
Ver solución (hacer click aquí)

10.- ¿Cuál es la probabilidad de que al ordenar en fila a 2 hombres y 2 mujeres, los 2 hombres estén juntos?
(a) 3/4
(b) 1/4
(c) 1/3
(d) 1/2
Ver solución (hacer click aquí)

ALGEBRA
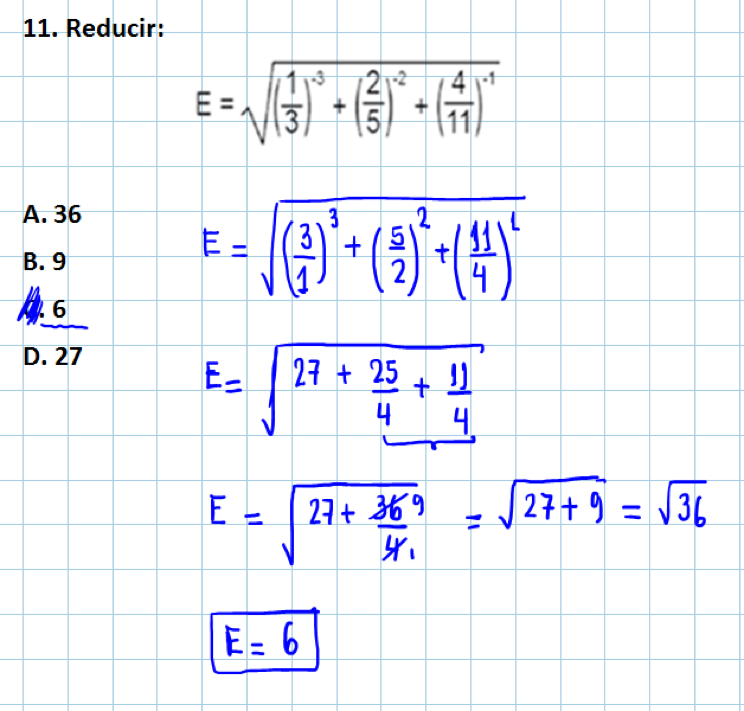
11.- Reducir:
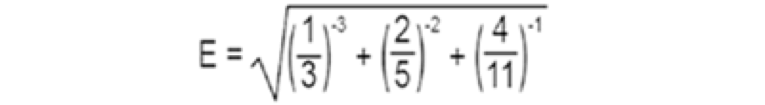
(a) 36
(b) 9
(c) 6
(d) 27
Ver solución (hacer click aquí)
12.-
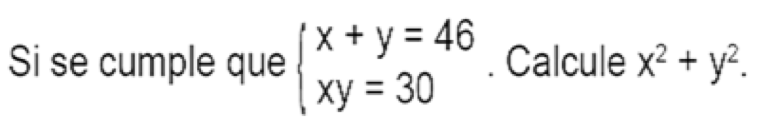
(a) 2116
(b) 2176
(c) 2056
(d) 2086
Ver solución (hacer click aquí)

13.- Si x1, x2 son las raíces de la ecuación, en variable x,
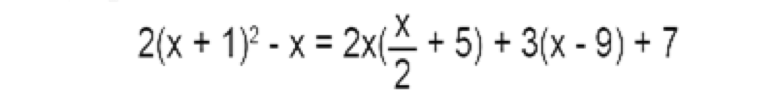
Halle x1 + x2
(a) 10
(b) - 10
(c) - 5
(d) 5
Ver solución (hacer click aquí)

14.- Considere el sistema de ecuaciones:

Halle x/y
(a) 32/5
(b) 27/32
(c) 27/5
(d) 32/27
Ver solución (hacer click aquí)

15.- Reduzca la siguiente expresión y dé como respuesta el numerador obtenido.
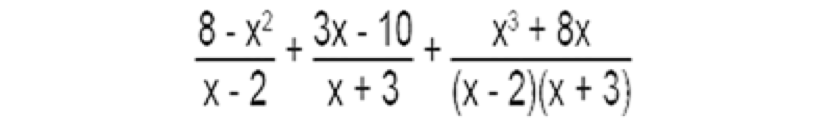
(a) 50
(b) 2
(c) 5
(d) 44
Ver solución (hacer click aquí)

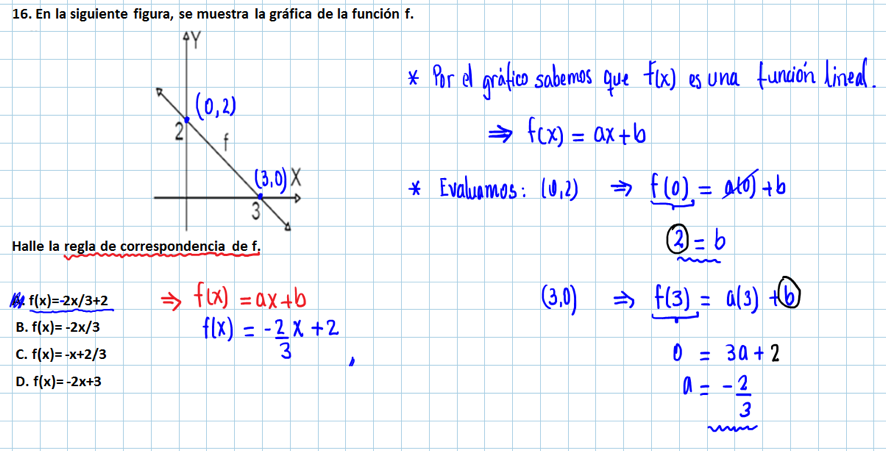
16.- En la siguiente figura, se muestra la gráfica de la función f.
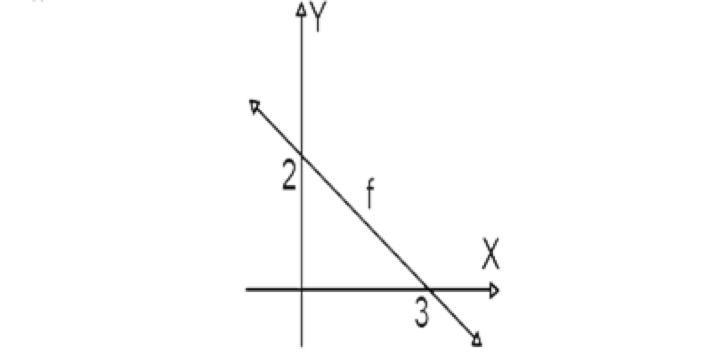
Halle la regla de correspondencia de f.
(a) f(x)= 2x/3+2
(b) f(x)= -2x/3
(c) f(x)= -x+2/3
(d) f(x)= -2x+3
Ver solución (hacer click aquí)
17.- A un paseo van 53 personas entre adultos y niños. Si el precio del pasaje de un adulto es S/.10, el de un niño es S/.7.5 y el costo del paseo es S/.480, calcule la diferencia entre la cantidad de adultos y niños.
(a) 11
(b) 12
(c) 13
(d) 14
Ver solución (hacer click aquí)

18.- Dada la igualdad
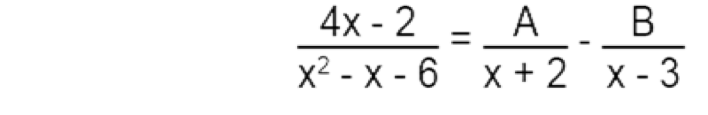
Halle: A + B.
(a) 2
(b) 3
(c) 0
(d) 1
Ver solución (hacer click aquí)

19.- Dentro de 33 años, la suma de las edades de una padre y su hijo, será 138 años. Si hace 10 años la diferencia de sus edades era 32 años, halle la edad actual del padre.
(a) 20 años
(b) 72 años
(c) 52 años
(d) 32 años
Ver solución (hacer click aquí)

20.- Si se cumple que: a + b = 15, a3 + b3 = 885 Halle: ab.
(a) 166
(b) 166/3
(c) 163/3
(d) 163
Ver solución (hacer click aquí)
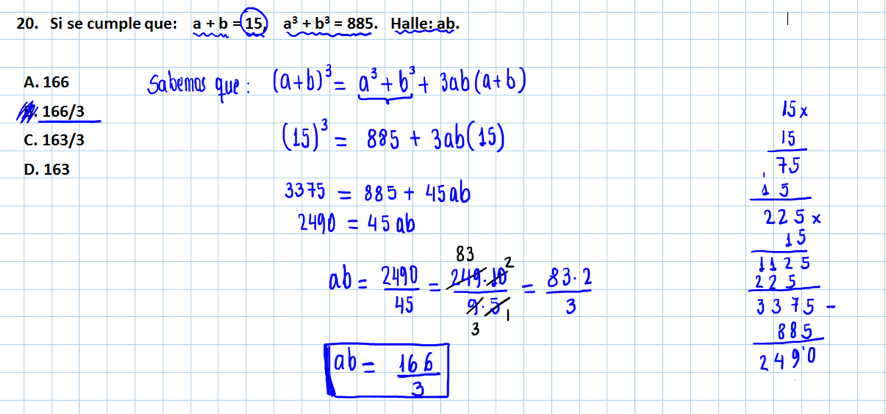
GEOMETRIA
GEOMETRÍA Y MEDIDA
21.- Convertir 9/π grados sexagesimales a radianes.
(a) 1/10 rad
(b) 1/5 rad
(c) 1/20 rad
(d) 1/4 rad
Ver solución (hacer click aquí)

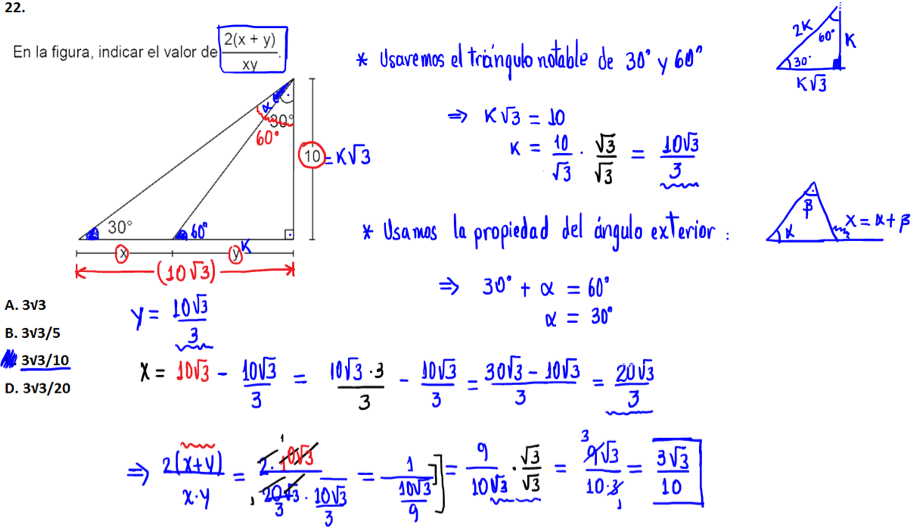
22.-
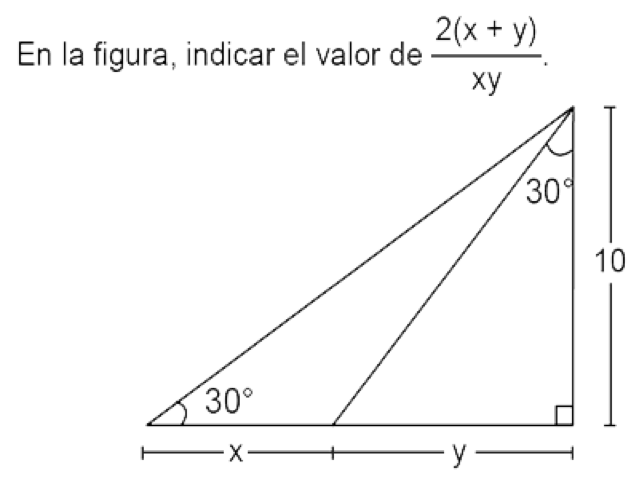
(a) 3√3
(b) 3√3/5
(c) 3√3/10
(d) 3√3/20
Ver solución (hacer click aquí)
23.- Un cuadrado y un hexágono regular tienen ambos un perímetro de 24 cm. Calcular la relación de sus áreas.
(a) √3/2
(b) √3
(c) √3/3
(d) √3/4
Ver solución (hacer click aquí)

24.- En un triángulo rectángulo ABC recto en B, la altura relativa a la hipotenusa es 6 y la proyección del cateto AB sobre la hipotenusa es 3. Calcular la suma de catetos.
(a) 6√5
(b) 9√5
(c) 12√5
(d) 15√5
Ver solución (hacer click aquí)

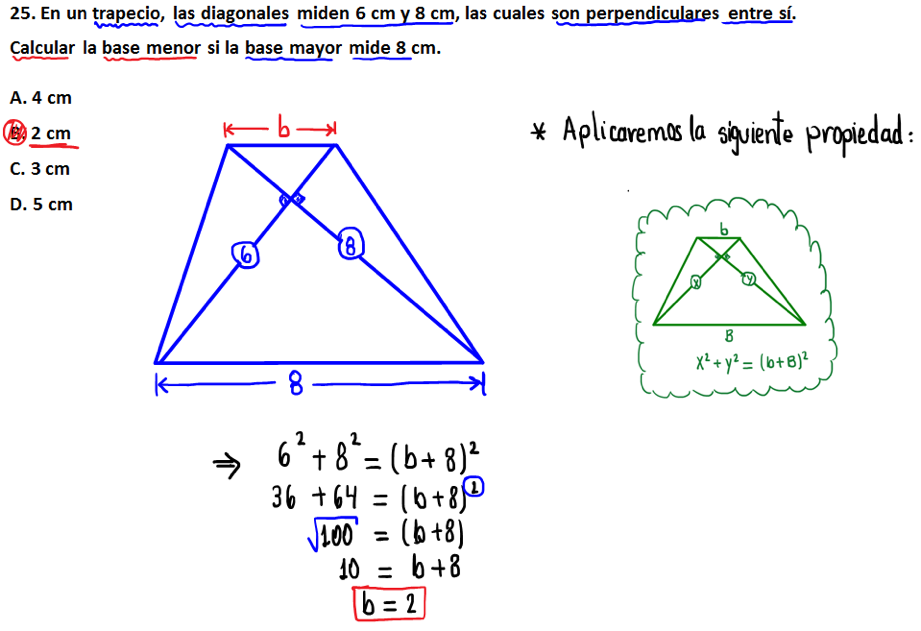
25.- En un trapecio, las diagonales miden 6 cm y 8 cm, las cuales son perpendiculares entre sí. Calcular la base menor si la base mayor mide 8 cm.
(a) 4 cm
(b) 2 cm
(c) 3 cm
(d) 5 cm
Ver solución (hacer click aquí)
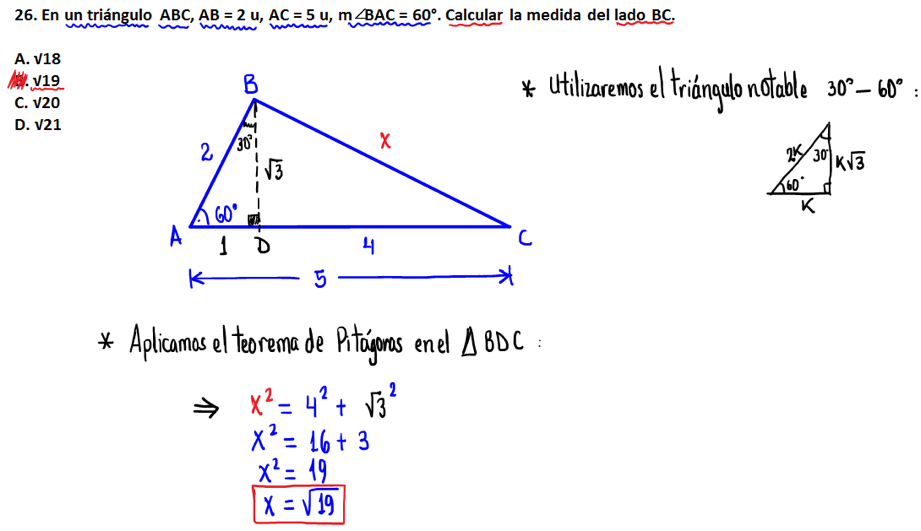
26.- En un triángulo ABC, AB = 2 u, AC = 5 u, m∠BAC = 60°. Calcular la medida del lado BC.
(a) √18
(b) √19
(c) √20
(d) √21
Ver solución (hacer click aquí)
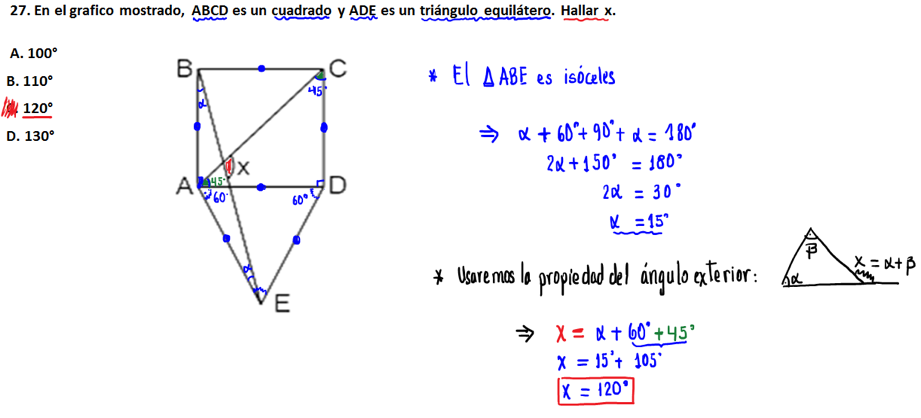
27.- En el grafico mostrado, ABCD es un cuadrado y ADE es un triángulo equilátero. Hallar x.
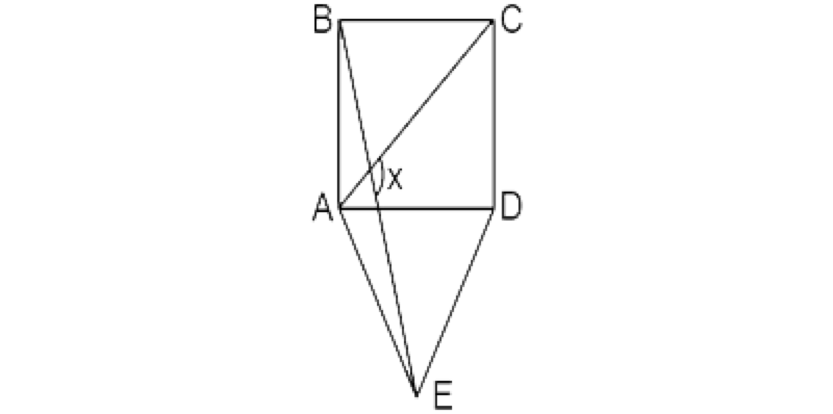
(a) 100°
(b) 110°
(c) 120°
(d) 130°
Ver solución (hacer click aquí)
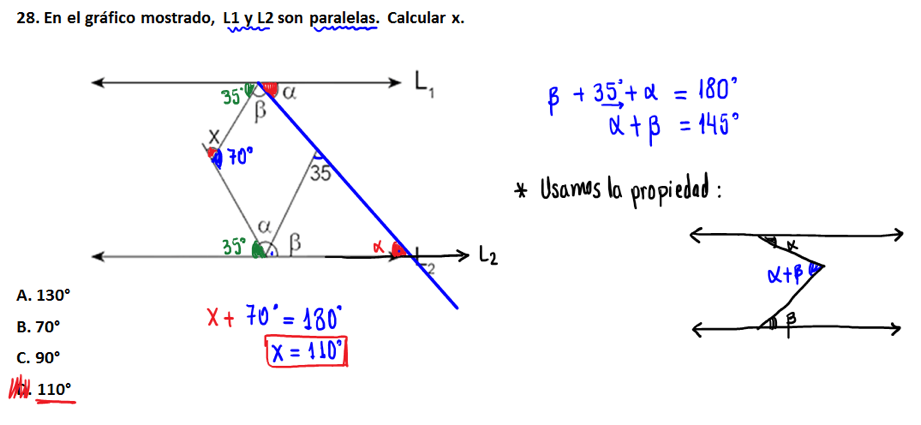
28.- En el gráfico mostrado, L1 y L2 son paralelas. Calcular x.
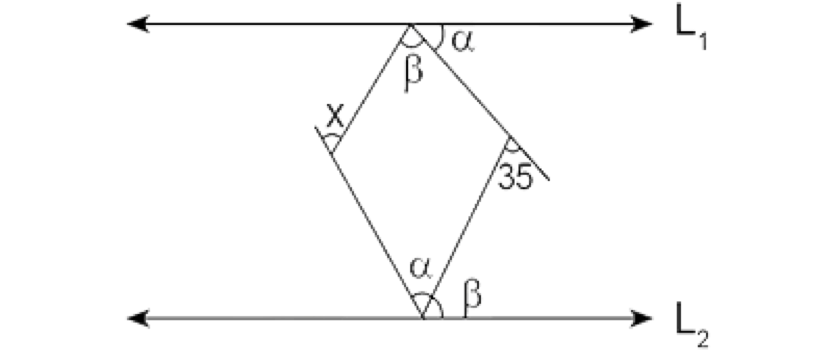
(a) 130°
(b) 70°
(c) 90°
(d) 110°
Ver solución (hacer click aquí)
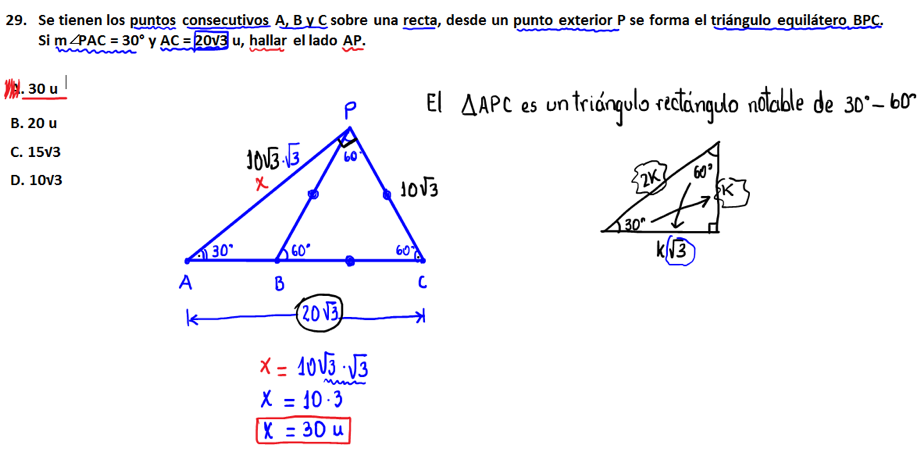
29.- Se tienen los puntos consecutivos A, B y C sobre una recta, desde un punto exterior P se forma el triángulo equilátero BP (c) Si m∠PAC = 30° y AC = 20√3 u, hallar el lado AP.
(a) 30 u
(b) 20 u
(c) 15√3
(d) 10√3
Ver solución (hacer click aquí)
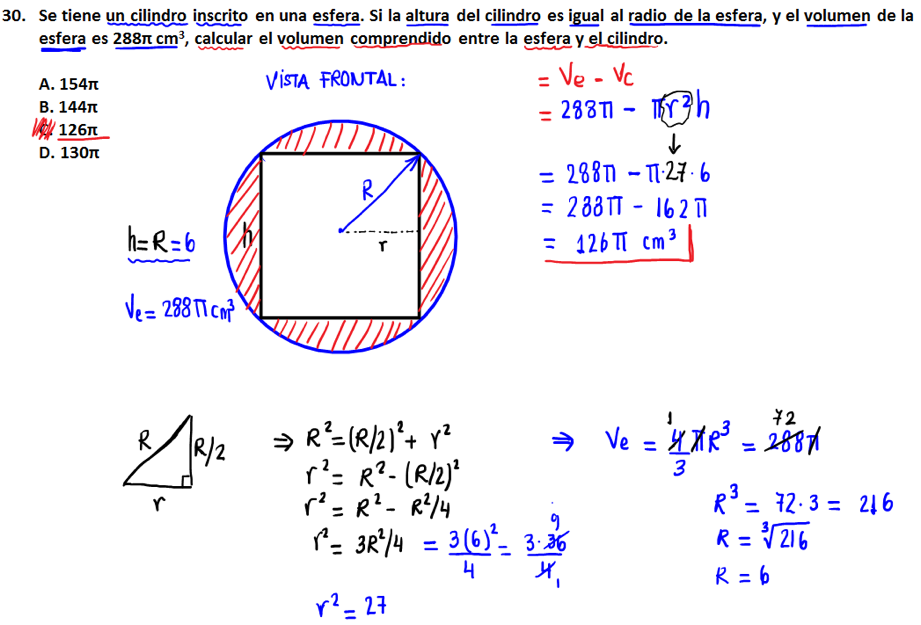
30.- Se tiene un cilindro inscrito en una esfer (a) Si la altura del cilindro es igual al radio de la esfera, y el volumen de la esfera es 288π cm3, calcular el volumen comprendido entre la esfera y el cilindro.
(a) 154π
(b) 144π
(c) 126π
(d) 130π
Ver solución (hacer click aquí)
Si quieren contribuir con sus propias soluciones, por favor contactenos al facebook de OportuniDar: https://www.facebook.com/OportuniDarPeru/
Gracias!